Fibonacci Spiral: Design Imitates Nature
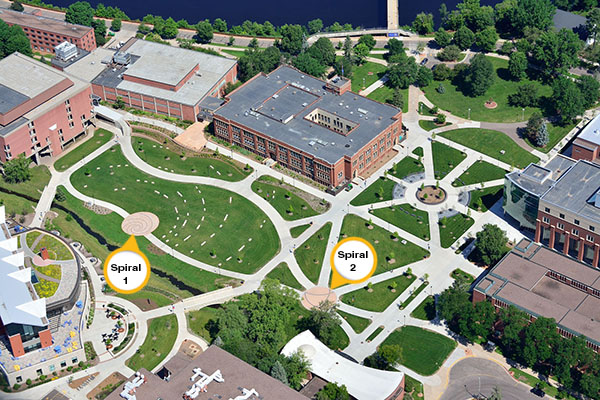It’s only appropriate that in a place devoted to higher education, even the site design should reflect the search for knowledge. The redesigned central campus at the University of Wisconsin-Eau Claire honors math, science, art – even music – with two Fibonacci spirals embedded in the South Schofield Lawn.
The spiral design begins with the Fibonacci sequence, named for an Italian mathematician (Leonardo de Pisa, known as Fibonacci), who introduced the sequence to western European mathematics in 1202; the sequence had been described even earlier in Indian mathematics. (Fibonacci also introduced Arabic numerals to Europe.)
The Fibonacci sequence begins like this:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
The next number is found by adding up the two numbers before it: 1+1=2, 1+2=3, 2+3=5, etc. So the next number in the sequence above would be 21+34=55.
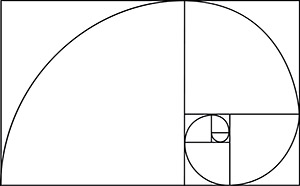When you draw the sequence as ever-increasing boxes, you create a Fibonacci rectangle. And then, if you connect the boxes with an ever-increasing spiral, you end up with a Fibonacci spiral. Why is this significant? The sequence appears throughout nature – from a tiny snail shell to the nodes of a pinecone to the storm clouds surrounding the eye of a hurricane to the spiraling stars of galaxies to the whorls of your own fingerprints. (For a helpful video, click here.)
A Fibonacci spiral in nature may certainly be beautiful, but it generally has a very utilitarian purpose. Consider the sunflower, which often is used as an example of Fibonacci spirals. The pattern of the sunflower seeds allows the flower to fit the most seed heads in the least space. Many other plants show leaves, branches, and/or petals growing in spirals, an adaptation that keeps new leaves from blocking the sun from older leaves, or allows the most rain or dew to reach the plant’s roots.
One of the Fibonacci spirals at UW-Eau Claire is easy to spot (spiral 1 in the image above). The tight spiral near the center of the South Schofield Lawn encompasses the decorative brick area and can be extended through the stone benches of this outdoor amphitheater. Although it’s slightly less immediately identifiable as a Fibonacci spiral, a second, more open spiral (spiral 2 above) lies at the convergence of six sidewalk segments near the center of the campus.
The Fibonacci form is embedded in education, so it’s only right to have it permanently embedded in an area that thousands of students, faculty, and staff walk through each day. The central campus design and its underlying infrastructure were featured in the latest issue of our TRENDS magazine.
Once you know what to look for, you’ll find Fibonacci spirals all around you. How many Fibonacci spirals can you spot today?
For more information, check the following:
The Fibonacci sequence in nature.
Math and the Fibonacci sequence.
Post a comment: